Three Part Math Lesson: Comet Halley

This a summary of the three-part problem solving lesson we observed in Laura's classroom.  The class had many opportunities to work in groups and share their thinking with each other prior to this visit.

This problem is taken from Nelson: Chapter 4 Problem Bank, question #5 (page 133)

Part One: Getting Started

Laura used a math string to activate her students' prior knowledge of addition and subtraction strategies.  Her goal was to highlight the 'common difference' strategy the class had been working on.

The math string was written on the blackboard for students to complete individually.

Once students completed the string individually, students shared their thinking with the class.  As students shared their strategy, Laura represented their thinking on the blackboard.

Part 2: Working on It
Laura introduced the problem to the class by sharing a personal experience about waiting to see Halley's comet as a child.

She then introduced the problem to the class:

Comet Halley is a periodic comet that is visible at regular intervals.  It was visible from Earth in 1758, 1834, 1910, and again in 1986.  How many more times will it be visible before the year 2500?

The whole class completed the KWC chart to ensure everyone understood the problem.

K- what you want to know, W- what you want to find out, C- conditions/rules of the problem

After the KWC chart was completed, students worked in pairs to solve the problem on chart paper.

While students worked on the problem, Laura circulated and identified the strategies and thinking she wanted to highlight during the consolidation.

Part 3: Consolidation (reflect and connect)
The first strategy Laura used to consolidate students' thinking was a GALLERY WALK.  This strategy allows everyone to participate and give students the opportunity to view each other's work.

After each pair was given the opportunity to walk around the room to look at other solutions and think about how their thinking was similar or different than the other pairs, they were given sticky notes to write any questions they might have about a particular strategy or solution and leave it on the chart paper.

Here are a few examples of what students wrote:

After the gallery walk, Laura strategically chose 3 pairs to share their thinking with the whole class.  Each pair's thinking highlighted a particular problem solving strategy.

During this MATH CONGRESS, students are encouraged to ask each other questions, make connections, or clarify each other's thinking.

Look for a Pattern

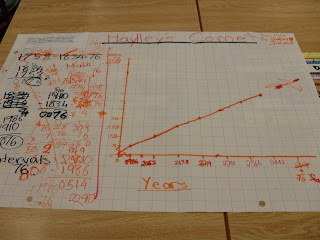Draw a Graph

Use algebraic thinking

Transition of one strategy into another.

After each pair shared their thinking with the whole class, Laura focused on the explicit teaching component of the lesson.  Since her learning goal for this lesson was to get students to use an equation to solve the problem, her explicit teaching focussed on clarifying the last pairs' solution.